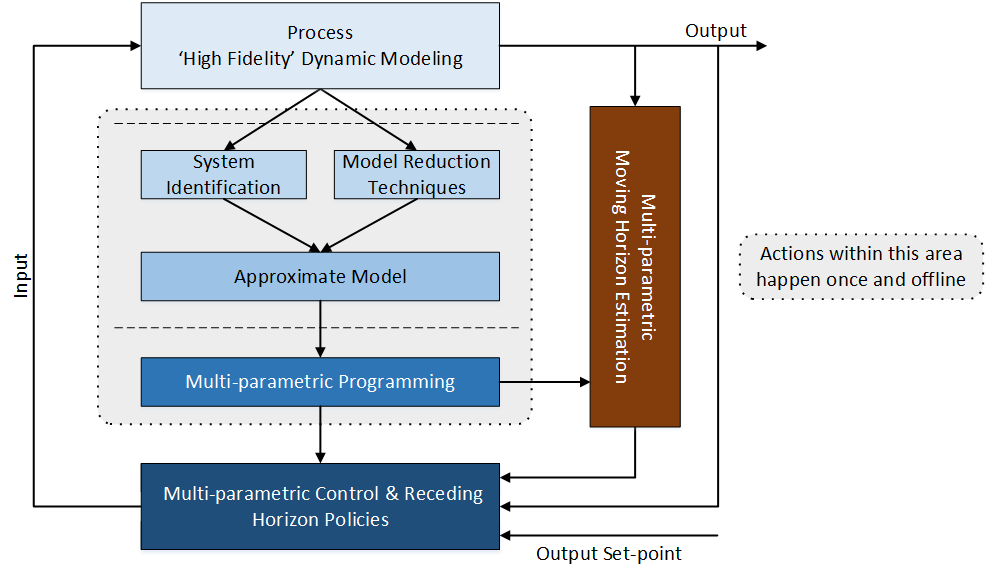
The PAROC Platform
The presence of uncertainty in process systems is one of the key reasons for deviation from set operation policies. As these uncertainties realize themselves on different time scales such as on a control, scheduling or design level, an integrated, comprehensive approach to consider uncertainty is required. Thus in this contribution we develop PAROC (PARametric Optimization and Control), a novel unified framework for the design, operational optimization and advanced model-based control of process systems, which decomposes this challenging problem into a series of steps, as shown in the Figure below.
The interested reader is encouraged to check out the recently introduced PAROC App prototype in the Software section. Click here to directly download the App.
Process 'High-Fidelity' Dynamic Modeling
The first step comprises the formulation of a high-fidelity dynamic model of the original process, as well as its validation using various techniques such as parameter estimation and dynamic optimization. This model does not only serve as the first step in translating a real-world system into a set of equations, but also as a platform for the validation of any receding horizon policy developed.
System Identification
A series of simulations of the high-fidelity model for different initial states is used to construct a meaningful linear state-space model of the process using statistical methods. One of the most widely applied tools within this area is the System Identification Toolbox from MATLAB® .
Model Reduction Techniques
While system identification relies on the user in terms of interpretation of the data and processing of the results, model-reduction techniques somewhat "automate" the reduction process based on formal techniques.
Approximate Model
While the high-fidelity model is in general applicable to design purposes, its complexity may render its use for the development of receding horizon policies computationally infeasible. Thus, in the second step, the validated high-fidelity model is reduced in complexity and size using system identification or advanced model reduction tools, while compromising the accuracy of the original model as little as possible. This approach results in a discretized state-space model, which is used in the next step for the development of receding horizon policies such as control laws and scheduling policies.
Multi-parametric Programming
At this step, based on the discretized state-space model, the problem of devising a suitable receding horizon policy is formulated as a constrained optimization problem. Within our framework, this problem is solved offline employing multi-parametric programming, where the states of the system are treated as parameters and the constrained optimization problem is solved as a function thereof. Due to the parameter-dependence of the constraints, different solutions might be optimal in different parts of the parameter space. This results in a partition of the parameter space into different regions, called critical regions, and each region is associated with a corresponding optimal solution of the optimization problem as a function of the parameters.
Multi-parametric receding horizon policies
As a result we obtain the receding horizon policies explicitly as a function of the states of the system1, and reduce the computational effort of their evaluation to a point location in the parameter space and a function evaluation.